This is a numerical problem on tool life in metal cutting or machining, which can be easily solved using Taylor’s Tool Life equation. This particular problem has two different parts. In the first part, the tool life is required to calculate for a given velocity. In the second part, velocity is required to calculate for a given tool life. Data for a combination of velocity and tool life is given. The exponent value (n) is also given. So let us first calculate Taylor’s constant (C) value.
Step-1: Calculate Taylor’s constant (C) value
It is given in the question that the tool shows 1 hr and 40 min tool life when used for cutting the specimen at 50 m/min cutting velocity. Therefore, from the three known values, the C can be calculated using Taylor’s Tool Life equation, as solved below.
T1 = 1 hr and 40 min = 100 min
V1 = 50 m/min
n = 0.28
So, the \(V{T^n} = C\) leads to:
\[\begin{array}{l}
{V_1} \times T_1^n = C\\
50 \times \left( {{{100}^{0.28}}} \right) = C\\
C = 181.54
\end{array}\]
Step-2: Tool life for 30% higher speed
As the tool material, workpiece material and cutting environment are unchanged, so the values of n and C will remain unaltered. Therefore, if the new velocity be V2 then:
\[{V_2} = 1.3{V_1} = 65\]
Say, the tool life be T2 for velocity V2. Again apply the Taylor’s Tool Life equation with the known values of V2, n and C to calculate T2 value.
\[\begin{array}{l}
{V_2} \times T_2^n = C\\
65 \times {\left( {{T_2}} \right)^{0.28}} = 181.54\\
{\left( {{T_2}} \right)^{0.28}} = 2.79\\
{T_2} = {\left( {2.79} \right)^{1/0.28}}\\
{T_2} = 39.18
\end{array}\]
Therefore, the tool life will reduce to 39.18 min if the same tool is used with at a speed 30% higher than previous one.
Step-3: Calculate cutting speed to get a life of 2 hr and 45 min
In this case, the required tool life is given as T3 = 2 hr and 45 min = 165 min. Once again, the values of n and C are unchanged as the tool material, workpiece material and cutting environment have not been changed. If the intended cutting velocity is V3, then it can be calculated as follows:
\[\begin{array}{l}
{V_3} \times T_3^n = C\\
{V_3} \times {\left( {165} \right)^{0.28}} = 181.54\\
{V_3} = 43.46
\end{array}\]
Therefore, the tool should be used at 43.46 m/min cutting velocity in order to obtain a tool life of 2 hr and 45 min.
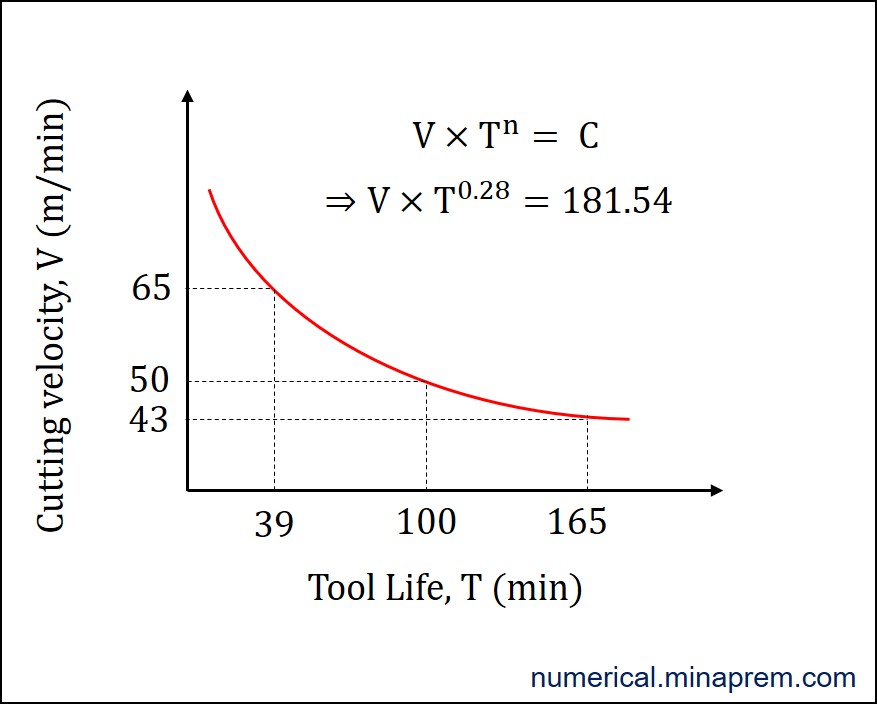
Now the solution is over. If you wish to plot the situation in a V-T curve, it will look like this. For 50 m/min cutting velocity, the tool life is 100 min. For 43.46 m/min cutting velocity, the tool life is 165 min. For 65 m/min cutting velocity, the tool life is 39.18 min.