Tool life indicates the duration of time within which a cutting tool provides satisfactory performance in machining. Taylor’s Tool Life equation provides the relationship between cutting velocity (V) and tool life (T) through a polynomial expression as given below. The constant n is called Taylorian Exponent, while constant C is known as Taylor’s Constant.
\[V{\left( T \right)^n} = C\]
Step-1: Speed to cutting velocity conversion
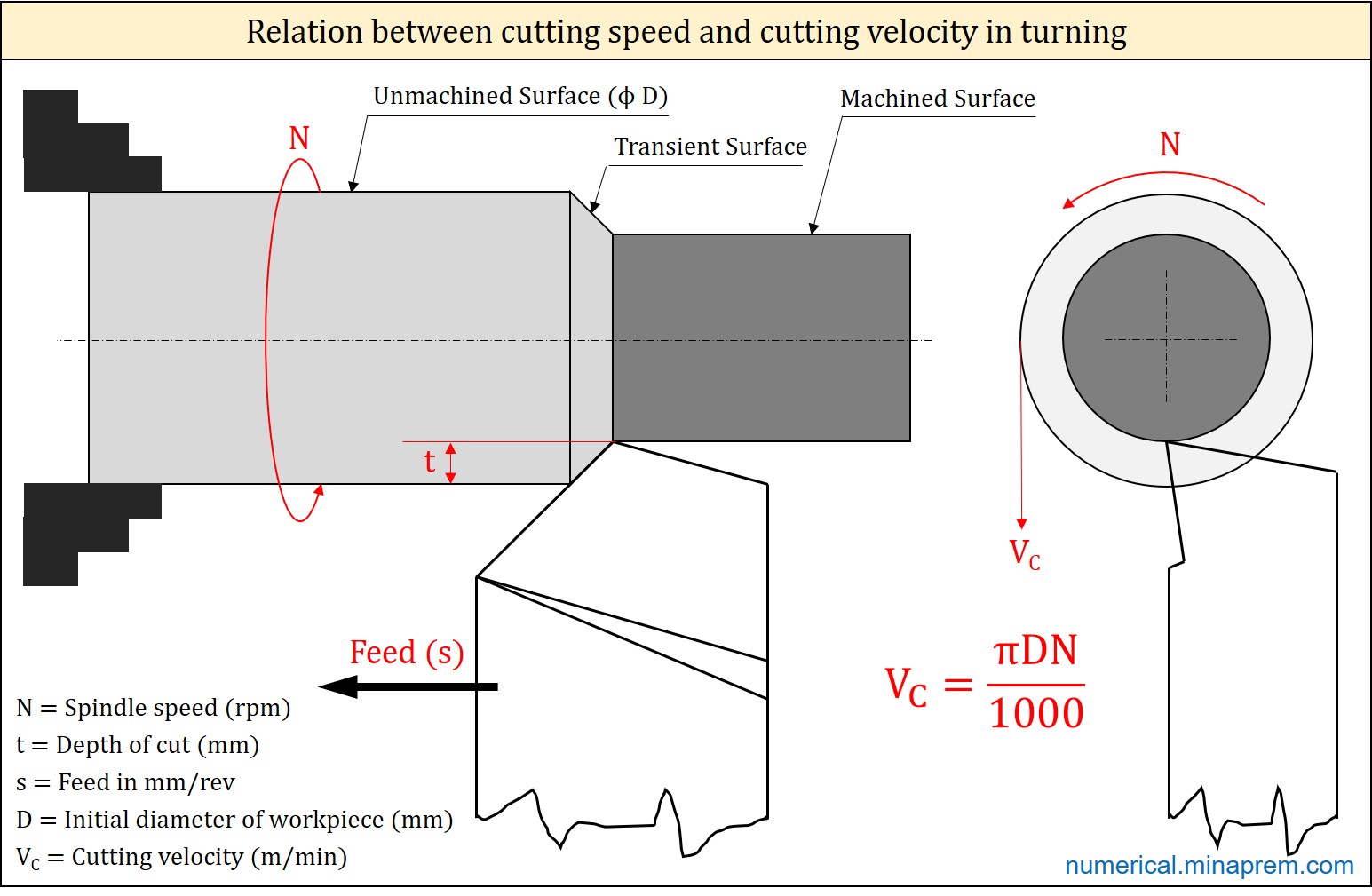
The Taylor’s Tool Life equation is based on the cutting velocity (V). However, speed values are given in the question. So it is first required to convert given speed values into cutting velocity. In case of straight turning operation in lathe, the rotational speed of job (N in rpm) can be converted to cutting velocity (V in m/min) using the workpiece diameter (D in mm), as given below.
\[V = \frac{{\pi DN}}{{1000}}\]
Step-2: Formulate the problem
In question, two speed values and the corresponding tool life values are given. Therefore, designating the cases as 1 and 2, the followings can be written.
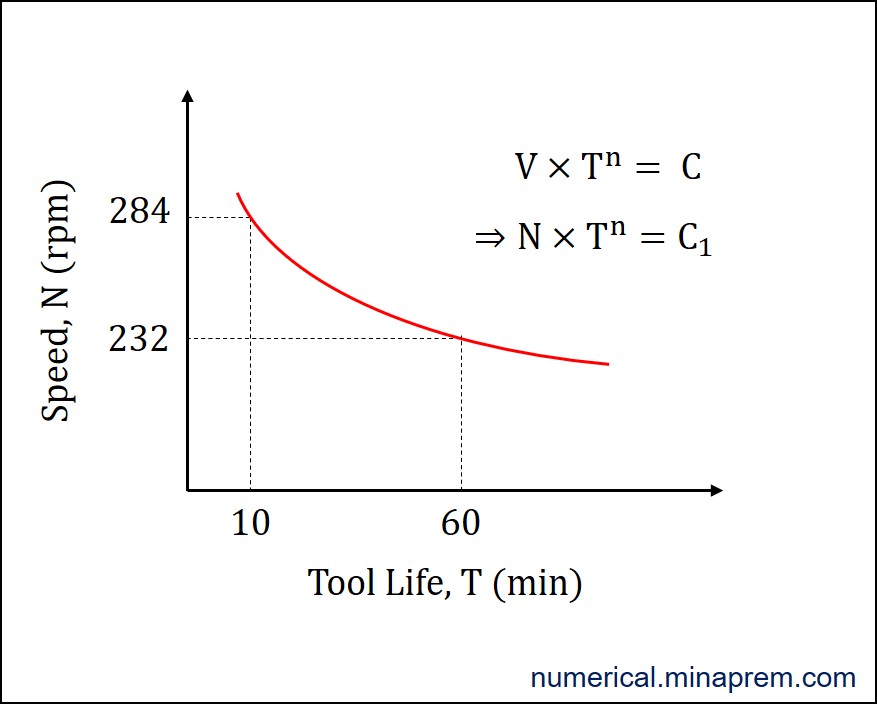
T1 = 10 min for N1 = 284 rpm
T2 = 60 min for N2 = 232 rpm
As the workpiece material, tool material, feed, depth of cut, and cutting environment are unchanged between the two given cases, so the constants n and C values of the Taylor’s Tool Life equation will remain same in both the cases. Accordingly, following two equations can be written.
\[{V_1}{\left( {{T_1}} \right)^n} = C\]
\[{V_2}{\left( {{T_2}} \right)^n} = C\]
Step-3: Calculating the value of Taylorian Exponent (n)
The value of n can be calculated by solving above two equations. For the same C, the left hand side of the above two equations can be equated. The velocity component can also be substituted with the speed following the above mentioned formula. The workpiece diameter is same for both the cases, and thus it will cancel out. Further solving the expressions taking logarithm, the n can be obtained. The solution is shown below.
\[\begin{array}{l}
{V_1}{\left( {{T_1}} \right)^n} = {V_2}{\left( {{T_2}} \right)^n}\\
\left( {\frac{{\pi D{N_1}}}{{1000}}} \right){\left( {{T_1}} \right)^n} = \left( {\frac{{\pi D{N_2}}}{{1000}}} \right){\left( {{T_2}} \right)^n}\\
{N_1}{\left( {{T_1}} \right)^n} = {N_2}{\left( {{T_2}} \right)^n}\\
\left( {\frac{{{N_1}}}{{{N_2}}}} \right) = {\left( {\frac{{{T_2}}}{{{T_1}}}} \right)^n}\\
\left( {\frac{{284}}{{232}}} \right) = {\left( {\frac{{60}}{{10}}} \right)^n}\\
\ln \left( {\frac{{284}}{{232}}} \right) = n\ln \left( {\frac{{60}}{{10}}} \right)\\
0.202 = n \times 1.792\\
n = 0.11
\end{array}\]
Therefore, the calculated value of Taylorian Exponent for the given case is n = 0.11. It is one unitless quantity.
It is also possible to plot the variation of tool life with speed, as shown below. All the constant terms can be subsumed in a new constant term (C1).
\[\begin{array}{l}
V{T^n} = C\\
\left( {\frac{{\pi DN}}{{1000}}} \right){T^n} = C\\
N{T^n} = \frac{{1000C}}{{\pi D}}\\
N{T^n} = {C_1}
\end{array}\]