This is a simple problem based on the Taylor equation of tool life. The Taylor’s Tool Life equation provides an exponential relationship between the cutting velocity and tool life, as given below. The V indicates cutting velocity (m/min), T indicates tool life (min), n is a unitless constant called Taylor’s Exponent, and C is another unitless constant called Taylor’s constant.
\[V{\left( T \right)^n} = C\]
Step-1: Formulate the problem to apply Taylor’s Tool Life equation
In the question, two cases are given – original one and with reduced velocity. Let us first designate the two cases by suffixes 1 and 2. Originally say the tool life was T1 with cutting velocity V1. After reduction of cutting speed by 50% (i.e. half of the previous one), say the velocity is V2 and the corresponding tool life is T2. Therefore, the following two points can be written.
(i) At V1, life is T1
(ii) At V2 = (V1 / 2), life is T2
The tool material, workpiece material, feed, depth of cut, and cutting environment are kept unchanged in between these two cases. Therefore, the value of constants n and C will remain same for both the cases. Thus the following two equations can be written after applying Taylor’s Tool Life equation.
\[{V_1}{\left( {{T_1}} \right)^n} = C\]
\[{V_2}{\left( {{T_2}} \right)^n} = C\]
Step-2: Calculate the percentage increase in tool life when speed is reduced by 50%
The relation between original tool life and changed tool life can be easily obtained by solving above two equations. The left hand side of the above two equations can be made equal for same C value. The value of constants are given in the question as n = 0∙5 and C = 400 (though C data is superfluous as this value is not required to get the intended answer). The detailed solution is shown below.
\[\begin{array}{l}
{V_1}{\left( {{T_1}} \right)^n} = {V_2}{\left( {{T_2}} \right)^n}\\
\left( {\frac{{{V_1}}}{{{V_2}}}} \right) = {\left( {\frac{{{T_2}}}{{{T_1}}}} \right)^n}\\
\left\{ {\frac{{{V_1}}}{{\left( {\frac{{{V_1}}}{2}} \right)}}} \right\} = {\left( {\frac{{{T_2}}}{{{T_1}}}} \right)^{0.5}}\\
2 = {\left( {\frac{{{T_2}}}{{{T_1}}}} \right)^{0.5}}\\
\left( {\frac{{{T_2}}}{{{T_1}}}} \right) = {\left( 2 \right)^{1/0.5}}\\
\left( {\frac{{{T_2}}}{{{T_1}}}} \right) = 4\\
{T_2} = 4{T_1}
\end{array}\]
Therefore, the tool life will increase to 4 times of the original one if the speed is reduced by 50%. Now let us calculate the percentage increase in tool life, as per the instruction in question. The percentage increase is:
\[\begin{array}{l}
\left( {\frac{{{T_2} – {T_1}}}{{{T_1}}}} \right) \times 100\\
\left( {\frac{{{T_2}}}{{{T_1}}} – 1} \right) \times 100\\
\left( {4 – 1} \right) \times 100\\
3 \times 100\\
300
\end{array}\]
Therefore, the tool life will increase 300% if the cutting speed is reduced by 50%.
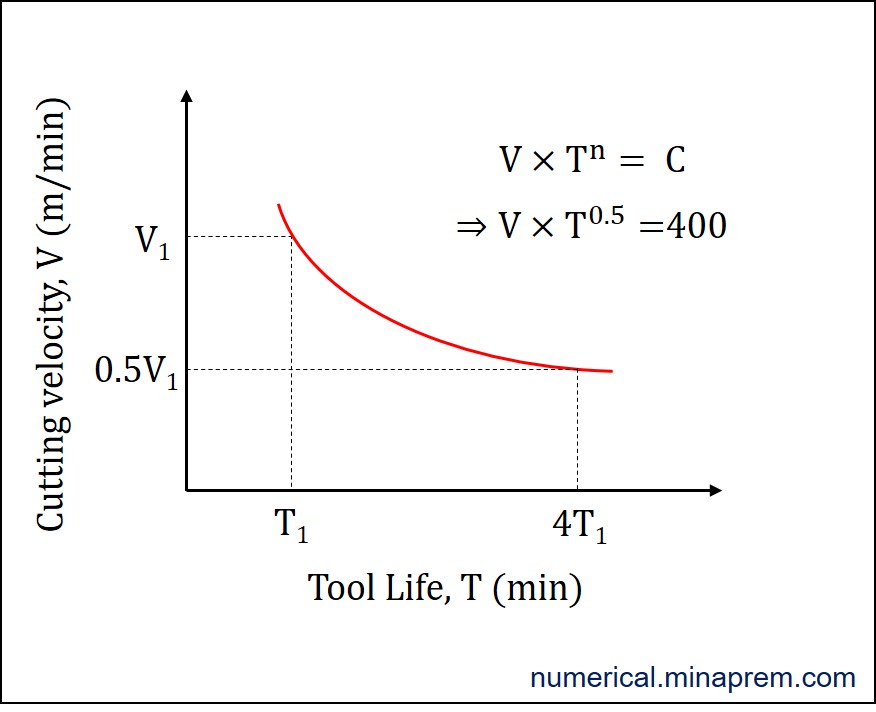
Now the intended answer is obtained. Moving ahead, from the given data it is also possible to draw the variation of tool life with velocity for the given case. The C value is already known as 400. A typical variation of tool life curve in V-T plot is shown below.