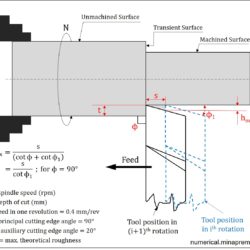
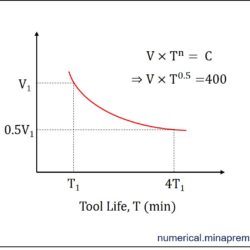
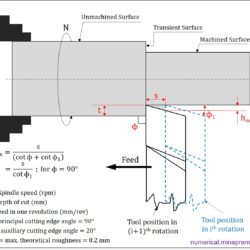
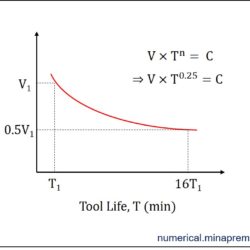
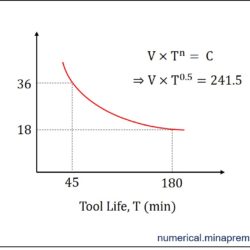
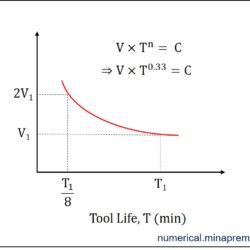
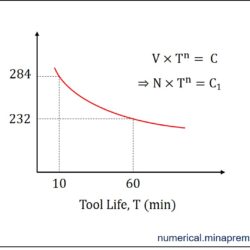
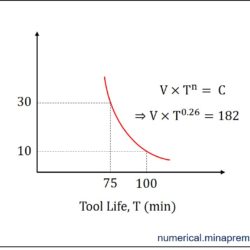
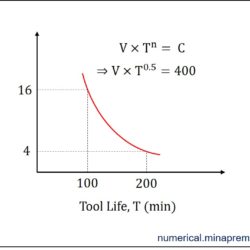
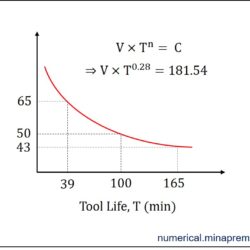
Surface roughness calculation in turning for sharp and nose radius tool
Question: In plain turning of a brass rod at a feed of 0.4 mm/rev, what will be the theoretical maximum surface roughness, if (i) the tool is relatively sharp with principal and auxiliary cutting edge angles of 90° and 20°, and (ii) the tool has a considerable nose radius of r = 1.0 mm. [Machining and Machine Tools by A. B. Chattopadhyay] This question is related to the calculation of