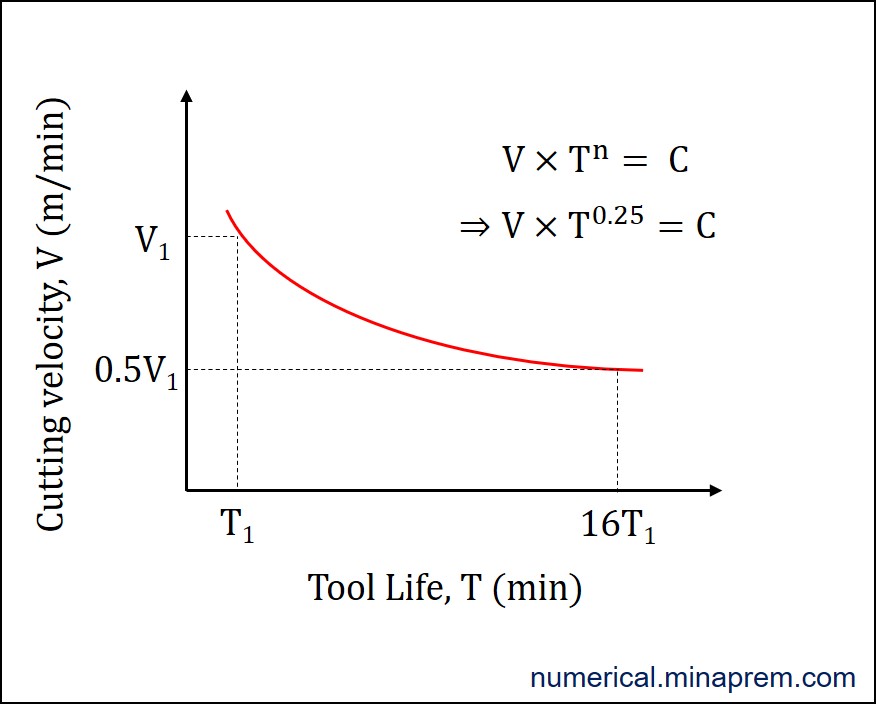
This problem related to the tool life in single point turning operation can be solved using the Taylor’s Tool Life equation. The well-known Taylor’s Tool Life equation provides an exponential relationship between the tool life and cutting velocity. The generalized form of this equation is shown below. Here V indicates cutting velocity (m/min), T indicates tool life (min), the constant n is called Taylor’s Exponent, and another constant C is called the Taylor’s constant.

\[V{(T)^n} = C\]

Step-1: Formulate the problem to apply Taylor’s Tool Life equation

Here two sets of velocity and tool life are available. Say, originally the cutting tool exhibits T₁ tool life when used under a velocity of V₁. Now, if the velocity is reduced by 50% then (say V₂) then the corresponding tool life is required to calculate. So the following two statements can be written.

(i) For T = T₁, the V = V₁

(ii) For T = T₂ = ?, the V = V₂ = (V₁ / 2)

In these two cases, the workpiece material, tool material, feed, depth of cut, and cutting environment are unchanged. Thus the value of constants n and C will remain same for the two cases. Accordingly, the following two equations can be written based on the generalised expression of Taylor’s Tool Life equation.

\[{V_1}{({T_1})^n} = C\]

\[{V_2}{({T_2})^n} = C\]

Step-2: Determine change in the tool life when cutting speed is reduced by 50%

The intended relation between T₁ and T₂ can be easily obtained by solving above two equations. The value of Taylor’s exponent (n) is given in the question as n = 0.25. So the left hand sides of the above two equations can be equated for the same C value. Further solution can fetch the intended relation between initial and changed tool life. The detailed solution is given below.

\[\begin{array}{l}
{V_1}{({T_1})^n} = {V_2}{({T_2})^n}\\
\left( {\frac{{{V_1}}}{{{V_2}}}} \right) = {\left( {\frac{{{T_2}}}{{{T_1}}}} \right)^n}\\
\left\{ {\frac{{{V_1}}}{{\left( {\frac{{{V_1}}}{2}} \right)}}} \right\} = {\left( {\frac{{{T_2}}}{{{T_1}}}} \right)^{0.25}}\\
2 = {\left( {\frac{{{T_2}}}{{{T_1}}}} \right)^{0.25}}\\
{\left( 2 \right)^{1/0.25}} = \left( {\frac{{{T_2}}}{{{T_1}}}} \right)\\
\frac{{{T_2}}}{{{T_1}}} = 16\\
{T_2} = 16{T_1}
\end{array}\]

Therefore, the tool life will increase by 16 times of the original value if the cutting velocity is reduced by 50%.

Now the intended solution is obtained. Progressing further for a detailed view, it is not possible to calculate the value of constant C from the given data in question. However, the typical variation of the tool life curve in a V-T plot can be drawn, as shown below.