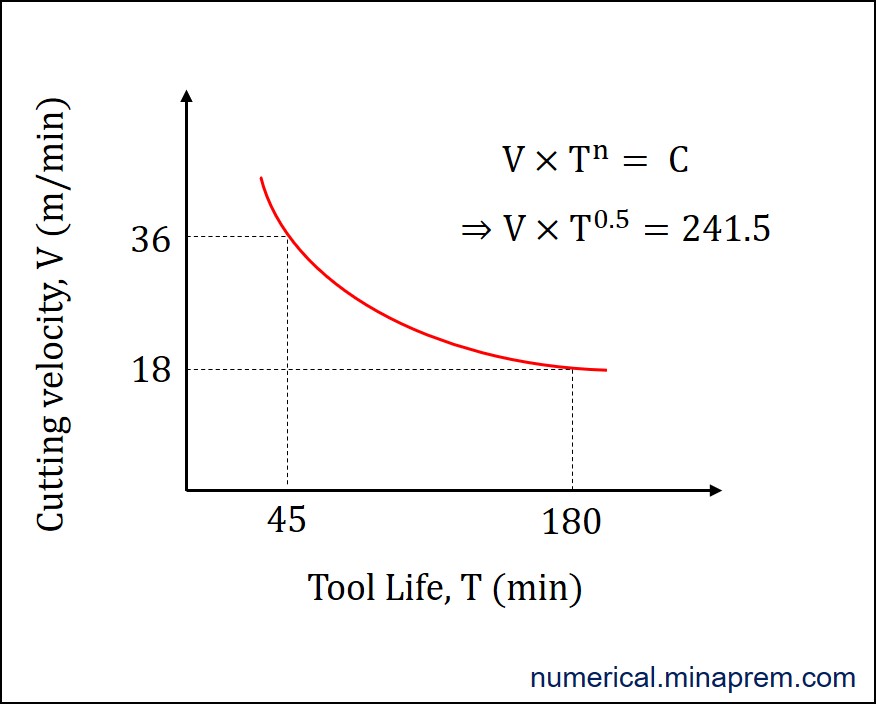
This is one simple problem based on Taylor’s Tool Life equation where one combination of velocity and life is given. It is required to find out cutting velocity to obtain 45 minutes life of the same tool used under unchanged condition. The value of Taylor’s exponent (n) is also given. Let us first designate the two given cases as 1 and 2. So the followings can be written based on the given values (T indicates tool life in min and V indicates cutting velocity in m/min).
(i) T1 = 180 min for V1 = 18 m/min
(ii) T2 = 45 min for V2 = ?
As the tool material, workpiece material, feed, depth of cut, and cutting environment are unchanged between the two given cases, so the value of constants n and C of the Taylor’s Tool Life equation will remain same. Therefore, the following equations can be written for the two given cases.
\[{V_1}{\left( {{T_1}} \right)^n} = C\]
\[{V_2}{\left( {{T_2}} \right)^n} = C\]
Step-1: Calculate the cutting speed for 45 minutes tool life
The intended cutting velocity (V2) can be easily obtained from the above two equations. Let us first equate the left hand sides of these equations for the same C value. The Taylor’s exponent (n) is given in the question as n = 0.5. Detailed solution is shown below.
\[\begin{array}{l}
{V_1}{\left( {{T_1}} \right)^n} = {V_2}{\left( {{T_2}} \right)^n}\\
\left( {\frac{{{V_2}}}{{{V_1}}}} \right) = {\left( {\frac{{{T_1}}}{{{T_2}}}} \right)^n}\\
\left( {\frac{{{V_2}}}{{18}}} \right) = {\left( {\frac{{180}}{{45}}} \right)^{0.5}}\\
{V_2} = 36
\end{array}\]
Therefore, the cutting speed (actually velocity) will be 36 m/min for the reduced tool life of 45 minutes.
Now the required value is obtained. It is also possible to calculate the Taylor’s Constant (C) value from the given data. This procedure is shown below. It is also possible to typically show the tool life curve in a V-T plot, as depicted below.
\[\begin{array}{l}
{V_1}{\left( {{T_1}} \right)^n} = C\\
18 \times {\left( {180} \right)^{0.5}} = C\\
C = 241.5
\end{array}\]