This is one simple problem that can be solved using Taylor’s Tool Life equation. In general, the tool life indicates the duration of time within which a cutting tool can provide satisfactory performance in machining. The well-known Taylor’s Tool Life equation provides the relationship between tool life (T) and cutting velocity (V) through an exponential equation as given below. The constant n is called Taylor’s Exponent, while another constant C is called Taylor’s constant.

\[V{T^n} = C\]

Step-1: Formulate the problem to apply Taylor’s Tool Life equation

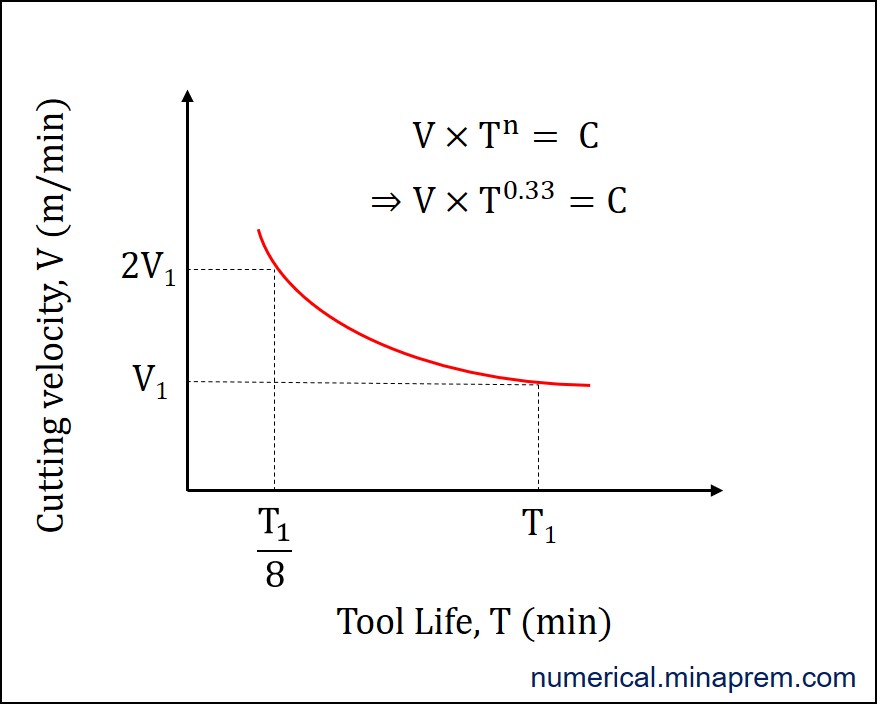
In question, two cases are given. Let us use notations 1 and 2 to specify the two cases. Originally, tool life is T₁ when cutting velocity is V₁. Now it is given in the question that doubling the cutting speed reduces the tool life to (1/8)^th of the original value. That means, for V₂ = 2V₁, the corresponding tool life reduces to T₂ = (T₁/8). In summary, the following two points can be written.

(i) At V = V₁, the T = T₁

(ii) At V = V₂ = 2V₁, the T = T₂ = (T₁/8)

As the tool material, workpiece material, feed, depth of cut, and cutting environment are unchanged between the two cases, the values of constants n and C will also remain same for these two cases. So, the Taylor’s Tool Life equation can be applied for both the cases with same n and C values, as given below.

\[{V_1}{\left( {{T_1}} \right)^n} = C\]

\[{V_2}{\left( {{T_2}} \right)^n} = C\]

Step-2: Solve for exponent n of the Taylor’s tool life equation

The objective is to get exponent n value. So, let us equate the left hand sides of the above two equations for the same C value. Further solution can fetch the n value directly. The detailed solution is shown below.

\[\begin{array}{l}
{V_1}{\left( {{T_1}} \right)^n} = {V_2}{\left( {{T_2}} \right)^n}\\
\left( {\frac{{{V_1}}}{{{V_2}}}} \right) = {\left( {\frac{{{T_2}}}{{{T_1}}}} \right)^n}\\
\left( {\frac{{{V_1}}}{{2{V_1}}}} \right) = {\left\{ {\frac{{\left( {\frac{{{T_1}}}{8}} \right)}}{{{T_1}}}} \right\}^n}\\
\left( {\frac{1}{2}} \right) = {\left\{ {\frac{1}{8}} \right\}^n}\\
\left( {\frac{1}{2}} \right) = {\left\{ {\frac{1}{2}} \right\}^{3n}}\\
1 = 3n\\
n = 0.33
\end{array}\]

Therefore, the required value of the exponent n in Taylor’s tool life equation is n = (1/3) = 0.33. It is one unitless quantity.

Now the intended values are obtained. From the given set of values in question, it is not possible to get the value of Taylor’s constant C. However, the variation of tool life with velocity can be visualized in a V-T curve, as depicted below.