In this problem, two cutting velocities and corresponding tool life values are given. The task is to calculate the index (or Taylor’s exponent, n). It can be calculated easily using Taylor’s tool life equation. Let us first designate the two given cases as 1 and 2. Therefore, the followings can be written from the given values.

T₁ = 10 min when V₁ = 100 m/min

T₂ = 30 min when V₂ = 75 m/min

Step-1: Apply Taylor’s tool life equation to calculate the value of index (n)

The Taylor’s tool life equation gives the relationship between the cutting velocity and tool life in a simplified way. It can be applied between two cases having unchanged workpiece material, tool material, feed, depth of cut and cutting environment. The well-known Taylor’s tool life equation is as follows.

\[V{\left( T \right)^n} = C\]

This equation can be rewritten in terms of given values, as follows:

\[{V_1}{\left( {{T_1}} \right)^n} = C\]

\[{V_2}{\left( {{T_2}} \right)^n} = C\]

Index (n) value can be obtained easily by solving these two equations. Let us equate the left hand sides of these two equations for the same C values, and further reduction can fetch n value. The solution is shown below.

\[\begin{array}{l}
{V_1}{\left( {{T_1}} \right)^n} = {V_2}{\left( {{T_2}} \right)^n}\\
\left( {\frac{{{V_1}}}{{{V_2}}}} \right) = {\left( {\frac{{{T_2}}}{{{T_1}}}} \right)^n}\\
\left( {\frac{{100}}{{75}}} \right) = {\left( {\frac{{30}}{{10}}} \right)^n}\\
\ln \left( {\frac{{100}}{{75}}} \right) = n\ln \left( {\frac{{30}}{{10}}} \right)\\
0.287 = n \times 1.098\\
n = 0.26
\end{array}\]

Therefore, the intended value of index is n = 0.26. It is one unitless quantity.

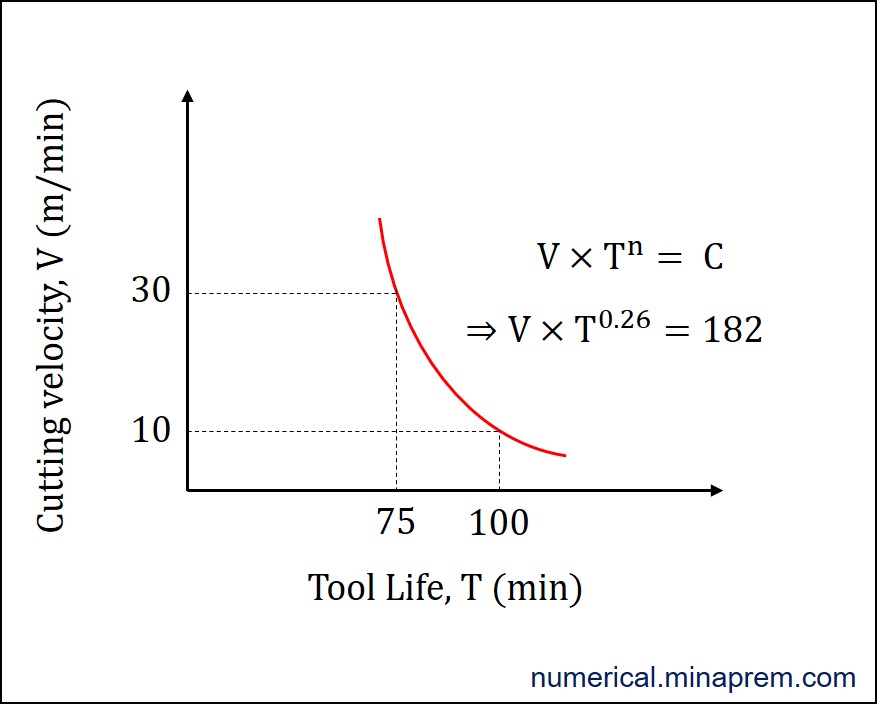
Curve for the Taylor’s Tool Life equation

Now the intended value is calculated. It is also possible to obtain the Taylor’s constant (C) value, and plot the tool life curve in a V-T plot for the given case. The C value for the given case can be calculated as follows:

\[\begin{array}{l}
{V_1}{\left( {{T_1}} \right)^n} = C\\
100 \times {\left( {10} \right)^{0.26}} = C\\
C = 182
\end{array}\]

Once the values of n and C are known, the tool life for any cutting velocity can be calculated through the basic formula. For this particular case, the Taylor’s Tool Life equation can be written as follows. It is also possible to draw the graph in a V-T plot as displayed below.

\[V{\left( T \right)^{0.26}} = 182\]